Számrendszerek és feltételek

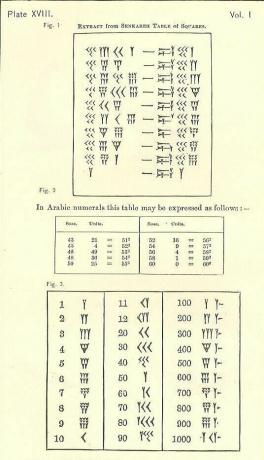
Három fő terület, amelyben különbözik a számunk

Képzelje el, milyen sokkal könnyebb lenne a számtani tanulást megtanulni a korai években, ha csupán annyit kellene tennie, hogy megtanulsz olyan sort írni, mint én és egy háromszöget. Ez alapvetően az összes Mesopotamia ősi emberének tennie kellett, bár ide-oda változtattak, meghosszabbítva, fordítva stb.

Nekik nem volt a tollaink és a ceruzaink, vagy a papíruk. Azt írták, hogy egy szerszámot használnának a szobrászatban, mivel a közeg agyag. Függetlenül attól, hogy ezt nehezebb vagy könnyebb megtanulni kezelni, mint a ceruzát, az csak felvágja, ám eddig a könnyű osztályon vannak, és csak két alapvető szimbólumot kell megtanulni.

A következő lépés csavarkulcsot dob ​​az egyszerűség osztályba. Használunk a 10. alap, egy fogalom, amely nyilvánvalónak tűnik, mivel tíz számjegyünk van. Valójában 20 van, de tegyük fel, hogy védő lábujjvédővel szandált viselünk, hogy ne kerüljünk bele a homokba a sivatag, meleg ugyanabból a napból, amely sütné az agyagtablettákat, és megőrizte őket, hogy évezredekig megtaláljuk őket később. A babilóniaiak használták ezt az alapot 10, de csak részben. Részben a Base 60-at használták, ugyanazzal a számmal, amit körülöttünk látunk percben, másodpercben és háromszög vagy kör fokozatában. Kiváló csillagászok voltak, és így a szám az ég megfigyeléseivel származhatott volna. A Base 60-nak különféle hasznos tényezői is vannak benne, amelyek megkönnyítik a kiszámítást. Ennek ellenére az, hogy meg kell tanulnunk a Base 60-ot, félelmetes.

A "Hálaadás Babilóniának" című részbenA Matematikai Közlöny, Vol. 76, 475, "A matematika történetének használata a matematika tanításában" (1992. március), pp. 158-178], Nick Mackinnon, az író-tanár azt mondja, hogy a babilóniai matematikát használja a 13 éves gyerekeknek a 10-től eltérő alapok megtanítására. A babiloni rendszer base-60-at használ, ami azt jelenti, hogy ahelyett, hogy tizedesje lenne, hanem szexuálisál.

A babiloni számrendszer és a miénk is az értékteremtés helyzetére támaszkodik. A két rendszer eltérően csinálja, részben azért, mert rendszerük nulla volt. A babiloni balról jobbra (magasról az alacsonyra) helyzetmeghatározó rendszer megtanulása az alapvető aritmetika első ízlése szempontjából valószínűleg nem több nehéz, mint megtanulnunk a kétirányút, ahol nem szabad megfeledkeznünk a tizedes számok sorrendjéről - a tizedesből növekvő, egy, tíz, száz, és aztán a másik oldalról a másik irányba száguldozik, nincs oneth oszlop, csak tized, század, ezred, stb

A következő oldalakon megyek a babiloni rendszer pozícióira, de először van néhány fontos számú szó, amelyet meg kell tanulnom.

Az évszakokról beszélünk tizedes mennyiségekkel. Van egy évtizedünk 10 évre, század 100 évre (10 évtizedre) vagy 10X10 = 10 év négyzetre, és évezred 1000 évre (10 évszázadra) vagy 10X100 = 10 év kockára esve. Nem tudok ennél magasabb kifejezést, de ezek nem az egységek, amelyeket a babilónia használ. Nick Mackinnon egy Sir Henry Rawlinson (1810-1895) (Senkareh (Larsa)) táblagépére utal, a babiloniaiak által használt egységekre, nemcsak az érintett évekre, hanem a feltételezett mennyiségekre is:

1. Soss
2. ner
3. sar.

sossnersosssarsoss

Még mindig nincs nyakkendő: Ez nem feltétlenül könnyebb megtanulni a négyzet és kockás év kifejezések származtatását latinul, mint egy egytagos babilón nyelvű, amelyek nem járnak kockázással, hanem szorzással 10.

Mit gondolsz? Nehezebb lett volna megtanulni a szám alapjait babilón iskolás gyerekként vagy modern hallgatóként egy angol nyelvű iskolában?

* George Rawlinson (1812-1902), Henry testvére, egyszerűsített átiratú négyzettáblát mutat Az ókori keleti világ hét nagy monarchia. A táblázat csillagászatinak tűnik, a babilóniai évek kategóriáin alapul.

Minden fénykép a George Rawlinson 19. századi kiadásának online beolvasott verziójából származik Az ókori keleti világ hét nagy monarchia.

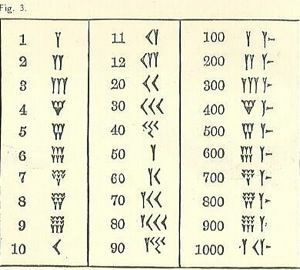
Mivel más rendszerrel nőttünk fel, a babilóniai számok zavaróak.

Legalább a számok balról magasról jobbra alacsonyra futnak, mint például az arab rendszerünkben, de a többi valószínűleg ismeretlennek tűnik. Az egyik szimbóluma ék vagy Y alakú. Sajnos az Y egy 50-öt is jelent. Van néhány különálló szimbólum (mindegyik az éken és a vonalon alapul), de az összes többi szám tőlük van kialakítva.

Ne felejtse el az írás formája ékírásos vagy ék alakú. A vonalak húzásához használt eszköz miatt korlátozott a változatossága. Az éknek farok lehet vagy nem lehet, és úgy húzza meg, hogy az ékírásos íróceruzát az agyag mentén húzza, miután a háromszög alakú részt lenyomta.

A 10, amelyet egy nyílfejjel neveznek, úgy néz ki, mint egy

Három sor, legfeljebb 3 kicsi 1-es (írva, mint Y-k, rövidített farokkal) vagy 10-es (egy 10-et írva, mint

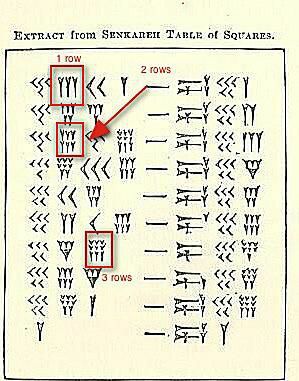
Három halmazállapotú szám van klaszterek kiemelve a fenti ábrán.

Jelenleg nem az értékükkel foglalkozunk, hanem azzal, hogy megmutassuk, hogyan láthatja (vagy írhatja) ugyanazon szám 4–9 helyét, összesítve. Három megy egymás után. Ha van egy negyedik, ötödik vagy hatodik, akkor az alul lesz. Ha van hetedik, nyolcadik vagy kilencedik, akkor harmadik sorra van szüksége.

A következő oldalak a Babilóniai énekes alak számításának elvégzésével kapcsolatos útmutatásokkal folytatódnak.

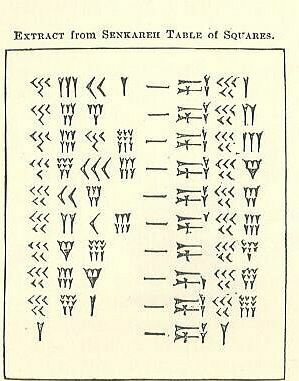
Amit fent olvasott a Soss - amire emlékezni fogsz a babilóniai 60 éve, az ék és a nyíl fej - amelyek leíró nevei a cuneiform jeleknek, nézd meg, kitalálhatod, hogyan működnek ezek a számítások. A kötőjellegű jel egyik oldala a szám, a másik pedig a négyzet. Próbálja ki csoportként. Ha nem tudja kitalálni, nézd meg a következő lépést.

Meg tudja találni most? Adj neki egy esélyt.

...

A bal oldalon 4 tiszta oszlop található, amelyet egy vonalszerű jel követ, és a jobb oldalon 3 oszlop található. A bal oldalról nézve az 1s oszlop ekvivalens valójában a "kötőjelhez" legközelebb eső 2 oszlop (belső oszlopok). A másik 2 külső oszlopot együtt számoljuk a 60-as évek oszlopának.

• A 4-
• A 3-Y = 3.
• 40+3=43.
• Az egyetlen probléma itt az, hogy mögöttük van egy másik szám. Ez azt jelenti, hogy nem egységek (a helyek). A 43 nem a 43, hanem a 43-60, mivel ez a szexuálisimális (base-60) rendszer, és a Soss oszlop, amint az alsó táblázat jelzi.
• Szorozzuk meg a 43-t 60-tal, hogy 2580-at kapjunk.
• Adja hozzá a következő számot (2
• Most 2601 van.
• Ez az 51-es négyzet.

A következő sorban 45 van Soss oszlopban, tehát megszorozzuk a 45-et 60-tal (vagy 2700-tal), majd hozzáadjuk a 4-et az egységek oszlopból, így 2704 lesz. A 2704 négyzetgyöke 52.

Meg tudja tudni miért az utolsó szám = 3600 (60 négyzet)? Tipp: Miért nem 3000?